2018-06-26

ボルツマンマシンについて勉強した　その１

機械学習ボルツマンマシン確率統計

はじめに

ボルツマンマシンについて勉強したからメモ．きっかけは離散変数をつかったVAEの論文を掘っていったら出会ったから．教科書としては以下の２冊を使った（ボルツマンマシンに関して内容はモロ被りなので好み）．

深層学習 (機械学習プロフェッショナルシリーズ)

作者: 岡谷貴之
出版社/メーカー: 講談社
発売日: 2015/04/08
メディア: 単行本（ソフトカバー）
この商品を含むブログ (13件) を見る

機械学習スタートアップシリーズこれならわかる深層学習入門 (KS情報科学専門書)

作者: 瀧雅人
出版社/メーカー: 講談社
発売日: 2017/10/21
メディア: 単行本（ソフトカバー）
この商品を含むブログ (1件) を見る

ここでは隠れ変数無し，あり2種類のボルツマンマシンの学習方程式の導出まで．

ボルツマンマシン（隠れ変数無し）

ボルツマンマシンは生成モデルの一つであり，無向グラフに対応した確率モデル．各ノードが確率変数 $x_i$ を持っており，エッジは重み $w_{ij}$ を持つ．ただし，無向グラフなため $w_{ij}=w_{ji}$ が成り立ち，自分自身とのコネクションは無し( $w_{ii}=0$ )．

ボルツマンマシンの表現には様々なものがあるが，まずは隠れ変数が無く確率変数 $x=[x_1,...,x_M]$ が2値（ $x\in\{0,1\}$ ）のボルツマンマシンを考える．ボルツマンマシンのモデルパラメータを $\theta$ とすると以下のように記述される．

$\displaystyle p(x|\theta)=\frac{\exp(-\Phi(x,\theta))}{Z(\theta)} \\ \displaystyle Z(\theta) = \sum_x\exp(-\Phi(x,\theta))$

$\Phi(x,\theta)$ はエネルギー関数と呼ばれるもので以下の形を取る．

$\displaystyle \Phi(x,\theta)=-\sum_ib_ix_i-\sum_{(i,j)\in\varepsilon}w_{ij}x_ix_j \\ \displaystyle =-\mathbf{b}'\mathbf{x}-\frac{1}{2}\mathbf{x}'\mathbf{W}\mathbf{x}$

$\varepsilon$ はエッジの集合．2行目の式は内積を用いて書き直したもので，第２項は重み行列 $\mathbf{W}$ が対称行列であり変数の順序は考えない( $w_{ij}x_ix_j=w_{ji}x_jx_i$ )ことと，対角成分が0であることを利用した．ただし，転置記号に $x'$ を用いて，ベクトルを小文字のボールド体，行列を大文字のボールド体で記述してる．また，ベクトルは基本的に列ベクトルを考え，行ベクトルは列ベクトルの転置としている．

$Z(\theta)$ は規格化定数で $P(x|\theta)$ の $x$ に対する和を1にしている．そのため， $Z(\theta)$ の右辺にある和は全ての $x$ に関する話になるので陽に書き下すと以下のようになる．

$\displaystyle Z(\theta)=\sum_{x_1=0,1}...\sum_{x_M=0,1}\exp(-\Phi(x,\theta))$

上記式から分かるように， $Z(\theta)$ は $2^M$ 要素の和から成り立つ．

ボルツマンマシン（隠れ変数あり）

次に隠れ変数がある場合について．観測された変数を持つノードだけでなく，隠れ変数を持つノードが存在するグラフを考える．隠れ変数は内部状態を表すものなので観測データには関係がない．ここで観測データに対応した変数を可視変数 $v=(v_1,v_2,...)$ とし，隠れ変数を $h=(h_1,h_2,...)$ とする．ここでこの二つの変数を一つにまとめた $x=(v_1,v_2,...,h_1,h_2，...)$ を導入すると，隠れ変数があるボルツマンマシンのエネルギー関数は隠れ変数が無い場合と同様に記述可能．

$\displaystyle \Phi(v,h,\theta)=\Phi(x,\theta)=-\mathbf{b}'\mathbf{x}-\frac{1}{2}\mathbf{x}'\mathbf{W}\mathbf{x}$

$x$ を使わず陽に書き表すと，

$\displaystyle \Phi(v,h,\theta)=-\mathbf{b}'\mathbf{v}-\mathbf{c}'\mathbf{h}-\frac{1}{2}\mathbf{v}'\mathbf{U}\mathbf{v}-\frac{1}{2}\mathbf{h}'\mathbf{V}\mathbf{h}-\mathbf{v}'\mathbf{W}\mathbf{h}$

となる．ただし，可視変数と隠れ変数に対し別々にモデルパラメータを定義した．また最後の項に $\frac{1}{2}$ がかかっていないのは $w_{ij}v_ih_j\neq w_{ji}h_iv_j$ であるため．エネルギー関数が定義できたのでモデル分布は

$\displaystyle P(v,h|\theta)=\frac{\exp(-\Phi(v,h,\theta))}{Z(\theta)}$

となる．

ここで，隠れ変数を積分消去した周辺分布について考える．周辺分布は

$\displaystyle P(v|\theta)=\sum_hP(v,h|\theta)=\frac{1}{Z(\theta)}\sum_h\exp(-\Phi(v,h,\theta))$

となる．ここで式の見通しをよくするため，この周辺分布に対するエネルギー関数を以下の形で表現する．

$\displaystyle \tilde{\Phi}(v,\theta)=-\log\sum_h\exp(-\Phi(v,h,\theta))$

すると周辺分布は

$\displaystyle P(v|\theta)=\frac{1}{Z(\theta)}\exp(\log(\sum_h\exp(-\Phi(v,h,\theta))))=\frac{\exp(-\tilde{\Phi}(v,\theta))}{Z(\theta)}$

と表現でき見通しがよくなる．

学習について（隠れ変数無し）

最尤推定による学習について考える．対数尤度関数を $L(\theta)=\sum_n\log P(v^{(n)}|\theta)$ とする．ただし， $n$ はサンプル数．最尤推定は尤度の最大化なので $\mathrm{arg}\max_\theta L(\theta)$ を解くことになる．よってパラメータ $\theta$ に関する微分に関する方程式 $\partial L(\theta)/\partial\theta =0$ の解を求めれば良い．バイアス $b_i$ に関する微分を計算すると，

$\displaystyle \frac{\partial}{\partial b_i}\sum_n\log P(v^{(n)}|\theta) \\ \displaystyle = \frac{\partial}{\partial b_i}\sum_n(\log(\exp(-\Phi(v,\theta)))-\log Z(\theta)) \\ \displaystyle = \sum_nv^{(n)}_i-\sum_n\frac{1}{Z(\theta)}\sum_vv_i\exp(-\Phi(v,\theta)) \\ \displaystyle = \sum_nv^{(n)}_i-N\sum_vP(v|\theta)v_i$

正規化定数はサンプルに依存しないため $\sum_n$ がサンプル数 $N$ 倍としてかける．ここで両辺をサンプル数 $N$ で割ると，

$\displaystyle \frac{1}{N}\frac{\partial L(\theta)}{\partial b_i} = \frac{1}{N}\sum_nv^{(n)}_i-\sum_vP(v|\theta)v_i$

と書き直すことができ，それにより第１項はサンプル平均，第２項はモデル分布に対する期待値として表現できる．そこで第１項を $\langle v_i\rangle_{\mathrm{data}}=1/N\sum_nv^{(n)}_i$ ，第２項を $\langle v_i\rangle_{\mathrm{model}}=\sum_vP(v|\theta)v_i$ として， $\frac{1}{N}\frac{\partial L(\theta)}{\partial b_i} = \langle v_i\rangle_{\mathrm{data}}-\langle v_i\rangle_{\mathrm{model}}$ と表す．

同様に重み $w_{ij}$ に関する微分も計算すると $\Phi(v,\theta)$ に関する微分についてしか違いがないため，バイアルに関する微分の係数のみが変わって，

$\displaystyle \frac{1}{N}\frac{\partial}{\partial w_{ij}}L(\theta)= \frac{1}{N}\sum_nv^{(n)}_iv^{(n)}_j-\sum_vP(v|\theta)v_iv_j=\langle v_iv_j\rangle_{\mathrm{data}}-\langle v_iv_j\rangle_{\mathrm{model}}$

となる．以上から隠れ変数のないボルツマンマシンの学習方程式は

$\displaystyle \langle v_i\rangle_{\mathrm{data}}=\langle v_i\rangle_{\mathrm{model}} \\ \displaystyle \langle v_iv_j\rangle_{\mathrm{data}}=\langle v_iv_j\rangle_{\mathrm{model}}$

となり，サンプルとボルツマンマシンの各統計量が一致すればいいことが分かる．ちなみに隠れ変数のないボルツマンマシンの対数尤度は凸なため，大域的最適解に収束する．

学習について（隠れ変数あり）

次に隠れ変数を持つボルツマンマシンの学習方程式を導出する．基本的には隠れ変数なしと同様で $\partial L(\theta)/\partial\theta =0$ を解くだけだが，隠れ変数は観測できない値なため周辺化した対数尤度 $\log P(v|\theta)=\log \sum_hP(v,h|\theta)$ について最尤推定を行う．ここでは隠れ変数と可視変数をまとめた $x$ を導入して，バイアスに関する微分を求める．

$\displaystyle \frac{\partial}{\partial b_i}\sum_n\log P(v^{(n)}|\theta)=\sum_n\frac{1}{P(v^{(n)}|\theta)}\frac{\partial}{\partial b_i}P(v^{(n)}|\theta)$

ここで $P(v^{(n)}|\theta)$ の $b_i$ に関する微分は，隠れ変数と可視変数をまとめた変数 $x_i$ を導入すれば

$\displaystyle \frac{\partial}{\partial b_i}P(v^{(n)}|\theta) \\ \displaystyle =\frac{\partial}{\partial b_i}\sum_h\frac{\exp(\mathbf{b}'\mathbf{x}+\frac{1}{2}\mathbf{x}'\mathbf{W}\mathbf{x})}{Z(\theta)} \\ \displaystyle =\sum_h\left(x_iP(x|\theta)-\frac{\exp(\mathbf{b}'\mathbf{x}+\frac{1}{2}\mathbf{x}'\mathbf{W}\mathbf{x})}{Z(\theta)^2}\frac{\partial Z(\theta)}{\partial b_i}\right) \\ \displaystyle =\sum_h\left(x_iP(x|\theta)-\frac{P(x|\theta)}{Z(\theta)}\sum_xx_i\exp(\mathbf{b}'\mathbf{x}+\frac{1}{2}\mathbf{x}'\mathbf{W}\mathbf{x})\right) \\ \displaystyle =\sum_hx_iP(x|\theta)-\sum_hP(x|\theta)\sum_xx_iP(x|\theta) \\ \displaystyle =\sum_hx_iP(x|\theta)-P(v^{(n)}|\theta)\sum_xx_iP(x|\theta)$

となる．これを元の式に代入すると，

$\displaystyle \frac{\partial}{\partial b_i}\sum_n\log P(v^{(n)}|\theta) \\ \displaystyle =\sum_n\frac{1}{P(v^{(n)}|\theta)}\left(\sum_hx_iP(x|\theta)-P(v|\theta)\sum_xx_iP(x|\theta)\right) \\ \displaystyle =\sum_n\left(\sum_hx_i\frac{P(x|\theta)}{P(v^{(n)}|\theta)}-\frac{P(v^{(n)}|\theta)}{P(v^{(n)}|\theta)}\sum_xx_iP(x|\theta)\right)$

ここで今後のために経験分布 $q(v)\equiv 1/N\sum_n\delta(x,x_n)$ を導入する．ただし， $\delta(x,y)$ はデルタ関数で $x$ と $y$ が一致するときに1を返す関数．

$\displaystyle \sum_n\left(\sum_hx_i\frac{P(x|\theta)}{P(v^{(n)}|\theta)}-\frac{P(v^{(n)}|\theta)}{P(v^{(n)}|\theta)}\sum_xx_iP(x|\theta)\right) \\ \displaystyle =N\sum_vq(v)\left(\sum_hx_iP(h|v,\theta)-\sum_xx_iP(x|\theta)\right)$

全体を $N$ で割ると最終的に対数尤度のバイアスに関する微分は

$\displaystyle \frac{1}{N}\frac{\partial L(\theta)}{\partial b_i}=\sum_v\sum_hx_iP(h|v,\theta)q(v)-\sum_vq(v)\sum_xx_iP(x|\theta)=\sum_v\sum_hx_iP(h|v,\theta)q(v)-\sum_xx_iP(x|\theta)$

となる．ただし，第２項目がサンプルと無関係なため $\sum_v$ を独立に計算できることと $\sum_vq(v)=1$ となる関係を使った．計算結果を見ると第１項目は $P(h|v,\theta)q(v)$ という分布の期待値になっており，第２項目は $\langle x_i\rangle_{\mathrm{model}}$ となっていることから，

$\displaystyle \frac{1}{N}\frac{\partial L(\theta)}{\partial b_i}=\mathbb{E}_{P(h|v,\theta)q(v)}[x_i]-\langle x_i\rangle_{\mathrm{model}}$

となる．

バイアスと同様に重みに関する微分を計算すると，隠れ変数のないボルツマンマシンと同様の関係が成り立つことから，

$\displaystyle \frac{1}{N}\frac{\partial L(\theta)}{\partial w_{ij}}=\mathbb{E}_{P(h|v,\theta)q(v)}[x_ix_j]-\langle x_ix_j\rangle_{\mathrm{model}}$

と求まり，隠れ変数を持つボルツマンマシンの学習方程式は

$\displaystyle \mathbb{E}_{P(h|v,\theta)q(v)}[x_i]=\langle x_i\rangle_{\mathrm{model}} \\ \displaystyle \mathbb{E}_{P(h|v,\theta)q(v)}[x_ix_j]=\langle x_ix_j\rangle_{\mathrm{model}}$

となる．

計算コストについて

隠れ変数あるなしのボルツマンマシンの学習方程式が求まり後は方程式を満たす $\theta$ を実際に計算するだけだが，一つ大きな問題がある．両ボルツマンマシンの学習方程式の右辺はモデル分布に対する期待値になっている．これを計算するには変数 $x$ に関する和を計算する必要があるが，それには $2^M$ 個の要素の和を計算しなければならない．これを計算することは（変数の次元にもよるが）ほぼ不可能なため，一般的にはサンプリングを用いて近似的に求める．

ということで次の記事ではサンプリングにより近似的に求める方法から．

2018-06-23

Concrete Distributionについて論文を読んだ

確率統計機械学習 VAE

はじめに

The Concrete Distribution: A Continuous Relaxation of Discrete Random Variablesを読んだのでメモ． ICLR2017の論文でGumbel Max Trickをベースに離散分布を連続分布に緩和することでVAEなどに応用しようというもの．Gumbel Max Trickについては以前に記事を書いた．

Concrete: CONtinuous relaxation of disCRETE

VAEでは正規分からサンプリングする際，reparameterization trickを使って微分可能な形でサンプリングをすることで正規分布をデータの分布として仮定したautoencoderを学習した．今回読んだ論文では正規分布のような連続分布ではなく離散分布（カテゴリカル分布）をデータの分布として仮定したいというもの．

カテゴリカル分布からのサンプリングにはGumbel Max Trickを使った方法がある．Gumbel Max TrickではGumbel分布からサンプリングされた摂動をカテゴリカル分布に加え，argmaxを取ることでカテゴリカル分布からサンプリングを行う．しかしargmaxの処理が入ってしまうため，backpropで勾配を計算する際にargmaxが取られたインデックスにしか勾配が伝播しないので，分布を正しく学習することができないという問題がある．そこでカテゴリカル分布を連続になるように緩和することで解決しようというのがConcrete: CONtinuous relaxation of disCRETE．別な言い方をすれば，Gumbel Max Trickでサンプリングされた値はone-hotベクトルになってしまう，すなわち単体上の頂点に位置するため，これを単体の内部に行くようにしようと言うのがconcrete．以下が例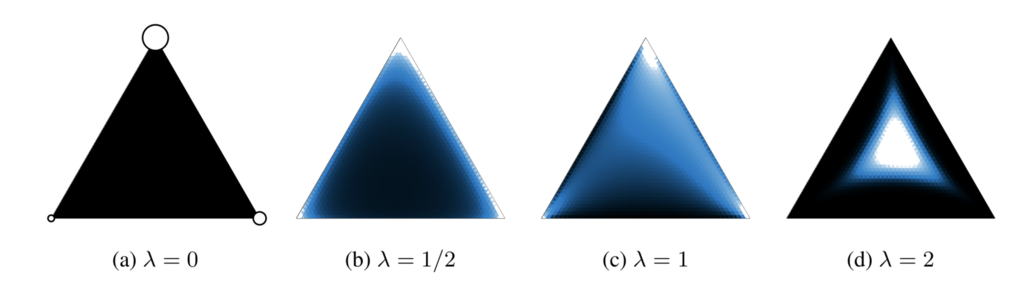． f:id:peluigi:20180623135205p:plain

どのように緩和するかという問題だが，argmaxの代わりにsoftmaxを使うだけ．とても単純．

$\displaystyle X = \mathrm{arg}\max(\alpha_k + G_k) \\ \displaystyle X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$

$\alpha_k$ はカテゴリカル分布のパラメータで $G_k$ は標準Gumbel分布からサンプリングされた値．重要なのが温度パラメータ $\lambda$ でこの値によって緩和の具合が変わる(上の図が $\lambda$ を変化させた時の例．大きくなるほど単体の中心に近付く)．上記緩和を使えばbackpropで勾配が伝播するので（誤解を招く言い方かもしれないが）分布の形状を正しく学習できる．上記の緩和を計算グラフにすると以下． f:id:peluigi:20180623140237p:plain このように確率分布からのサンプリングのノードが入った計算グラフをstochastic computation graphsというらしい．

ここで問題なのはargmaxを勝手にsoftmaxにしてしまったため，もはや確率変数 $X_k$ はカテゴリカル分布に従わない．そこで $X_k$ をconcrete random variableとし，この確率変数が従う分布Concrete Distributionを導入する．Concrete Distributionの密度関数は以下で定義される．

$\displaystyle p_{\alpha,\lambda}(x)=(n-1)!\lambda^{n-1}\prod_{k=1}^n\left(\frac{\alpha_kx_k^{-\lambda-1}}{\sum_{i=1}^n\alpha_ix_i^{-\lambda}}\right)$

この密度分布は以下のpropositionを満たす．

(a) (Reparametarization) $G_k\sim \mathrm{Gumbel}$ が $i.i.d$ なら $X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$

(b) (Rounding) $P(X_k\gt X_i$ $for$ $i\neq k)=\alpha_k/\sum_{I=1}^n\alpha_i$

(d) (Convex eventually) $\lambda\leq (n-1)^{-1}$ なら $p_{\alpha,\lambda}(x)$ はlog-convex

(a)に関してはそもそも $X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$ から定義されているので成り立つ．(b)と(c)も計算から求まって，元のカテゴリカル分布と一致する．(d)の証明に関してはスペースを使うので論文のAppendix参照．ただし(d)は重要で温度パラメータを決める一つの指標になる．

また，ここでは詳細は省くが，2クラスの場合(binary case)の導出も行なっており，その際には標準Gumbel分布ではなくLogistic分布からのサンプリング結果を摂動として与える(Gumbel分布の差がLogistic分布になるからとのこと)．

VAEへの応用

VAEへの応用を考える．カテゴリカル分布を使った際の損失関数は以下のようになる．

$\displaystyle L_1(\theta,a,\alpha)=\mathbb{E}_{D\sim Q_\alpha(d|x)} \left[\log\frac{p_\theta(x|D)P_a(D)}{Q_\alpha(D|x)}\right]$

$Q_\alpha$ は近似事後分布で $\alpha$ をパラメータとしたカテゴリカル分布．分子はカテゴリ $d$ とデータ $x$ の同時分布 $p_{\theta,\alpha}(x,d)=p_\theta(x|D)P_a(D)$ を表しており， $P_a(D)$ は $a$ をパラメータとするカテゴリカル分布．これをConcrete distributionを使って緩和することを考える．具体的には $D\sim \mathrm{Discrete}(\alpha(x))$ を $Z\sim \mathrm{Concrete}(\alpha(x),\lambda_1)$ とすることを考える．問題は，backpropを行うことができればいいため損失関数の緩和の方法は以下のように複数考えられる．

$\displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \\ \displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) +\sum_{i=1}^nZ_i \log\frac{p_{a}(d^{(i)})}{Q_{\alpha}(d^{(i)}|x)}\right] \\ \displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) \right] +\sum_{i=1}^nQ_\alpha(d^{(i)}|x) \log\frac{p_{a}(d^{(i)})}{Q_{\alpha}(d^{(i)}|x)}$

$d^{(i)}$ は $d_i^{(i)}=1$ を満たすone-hotベクトル．上記において一番上のみが以下のlower boundを保証する．

$\displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \leq \log\int p_\theta(x|z)p_{a,\lambda_2}(z)dx$

基本的にはいずれかの緩和された損失を適用すればいいが，愚直に用いるとunderflowを起こしてしまうので実装の際には以下のようにlog-spaceで計算を行う方がいいらしい．

$\displaystyle Y_k=\frac{\log\alpha_k+G_k}{\lambda}-\log\sum_{i=1}^n\exp\left\{\frac{\log\alpha_i+G_i}{\lambda}\right\} \\ \displaystyle \exp(Y)\sim Concrete(\alpha,\lambda) \\ \displaystyle Y\sim \mathrm{ExpConcrete}(\alpha,\lambda)$

またこの確率変数 $Y_k$ の密度関数（log-density）は以下で定義される．

$\displaystyle \log\kappa_{\alpha,\lambda}(y)=\log( (n-1)!)+(n-1)\log\lambda+\left(\sum_{k=1}^n\log\alpha_k-\lambda y_k\right)-n\log\sum_{k=1}^n\exp(\log\alpha_k-\lambda y_k)$

ということで実践的には上記のExpConcreteを使って緩和を行う．すると緩和された損失関数は以下のようになる．

$\displaystyle L_1(\theta,a,\alpha)\overset{\mathrm{relax}}{\leadsto} \\ \displaystyle = \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \\ \displaystyle = \mathbb{E}_{Y\sim\kappa_{\alpha,\lambda_1}(y|x)}\left[\log p_\theta(x|\exp(Y)) + \log\frac{\rho_{a,\lambda_2}(Y)}{\kappa_{\alpha,\lambda_1}(Y|x)}\right]$

この損失関数を使えばカテゴリカル分布をつかったVAEの学習ができる．論文のAppendixの最後にここで説明したConcreteとExpConcreteのほかに2クラスの場合(Binary case)のBinConcreteや実験で使われた分布がまとまったチートシートが書かれているので便利．またその他Appendixに実装の際や問題に適用する際のTipsが色々書いてあるので参考に．

終わり

今回読んだ論文とほぼ同じコンセプトのGumbel-softmaxというものが同時期にarxivに投稿されており，同様にICLR2017に採択されている．どっちもgoogle(deepmindとbrain)でなんだかなという気持ち．

あと，softmax入っているから温度係数が小さいと容易に勾配消失する気がするけど論文で言及されてなかった．時間を見て確認がてら実装したい．

2018-06-21

Gumbel Max Trickについて勉強した

確率統計機械学習

はじめに

Gumbel Max Trickについて勉強したからメモ． Gumbel Max Trickのお気持ちとしてはカテゴリカル分布から効率よくサンプリングしたいというもの(多分。。。)．言ってしまえばカテゴリカル分布におけるreparameterization trick．

accept-reject アルゴリズム

カテゴリカル分布からの基本的なサンプリング方法の一つにaccept-reject アルゴリズムがある．カテゴリカル分布のパラメータ（各カテゴリがサンプリングされる確率）を $\mathbf{\alpha}=\alpha_1,\alpha_2,...,\alpha_m$ とする． $u\sim\mathrm{Uniform}(0,\max\alpha_i)$ と $j\sim$ { $1,2,...,m$ } を一様にサンプリングし， $\alpha_j\geq u$ の時に $j$ を返し， $\alpha_j\lt u$ の時にはまたサンプリングを繰り返すというもの． $\alpha_j\lt u$ である限り二つの変数をサンプリングし続けなければならないから効率がわるい．

Gumbel Max Trick

Gumbel Max Trickでは標準Gumbel分布からカテゴリの数だけサンプリングを行い，得られた値を摂動としてカテゴリカル分布のパラメータに加えた後，argmaxを取ることでサンプリングをしようというもの．

$\displaystyle g_i \sim \mathrm{Gumbel}$

$\displaystyle j = \mathrm{arg}\max(\log\alpha_i+g_i)$

これならサンプリングの回数がカテゴリ数 $m$ になりaccept-reject アルゴリズムに比べ効率が良い．

Gumbel分布とは

突然出てきたGumbel分布だが，Gumbel分布は極値分布と呼ばれる分布の一つで，確率変数の最大値や最小値が従う分布らしい．極値分布の詳しい性質等は教科書とかで勉強しないと理解できなさそうなので割愛． Gumbel分布の密度関数と分布関数は以下で定義される．

$\displaystyle Gu_{\mu,\eta}(x)=\frac{1}{\eta}\exp\left(-\frac{x-\mu}{\eta}-\exp\left(-\frac{x-\mu}{\eta}\right)\right)$

$\displaystyle F_{\mu,\eta}(x)=\exp\left(-\exp\left(-\frac{x-\mu}{\eta}\right)\right)$

$\mu$ はlocation parameter， $\eta$ はscale parameterと呼ばれる分布のパラメータで，標準Gumbel分布の場合 $\mu=0,\eta=1$ となる．

なぜGumbel分布

ここで疑問になるのはなぜGumbel分布を使ってサンプリングができるのかということ．証明の方法は色々あるようだけど一番分かり易かったのがこれ．手順としては，location parameterが $\log(\alpha_i)$ ，scale parameterが1のGumbel分布からサンプリングされた値を $z_{1,...,m}$ とし， $z_i$ がもっとも大きくなる確率（すなわちiがサンプリングされる確率）が元のカテゴリカル分布のパラメータ $\alpha_i$ と一致すればいいでしょうというもの．すなわち

$\displaystyle P(z_i \mathrm{が最大}|z_i,\alpha_{1,..,m})=\alpha_i$

を証明する．location parameterが $\log(\alpha_i)$ のgumbel分布に関して考えているのは，locaton parameterが正規分布の平均と同様の役割をするため，VAEの論文で使用されている正規分布のreparameterization trickと同様に $Gu_{\log\alpha_i, 1}(x)=\log\alpha_i+Gu_{0,1}(x)$ と書けるから． $z_i$ はi.i.dにサンプリングされるため， $P(z_i \mathrm{が最大}|z_i,\alpha_{1,..,m})=P(z_i\gt z_1,...,z_i\gt z_m|\alpha_{1,...,m})=P(z_i\gt z_1|\alpha_1)...P(z_i\gt z_m|\alpha_m)$ と分解され， $P(z_i\gt z_j)$ はGumble分布の分布関数であることから

$\displaystyle P(z_i \mathrm{が最大}|z_i,\alpha_{1,..,m}) = \prod_{j\neq i}\exp(-\exp(-(z_i-\log\alpha_j)))$

と書直せる．さらにこれを $z_i$ に対して周辺化，すなわち $P(z_i \mathrm{が最大} | \alpha_{1,..,m}) = \int P(z_{i}|\alpha_{i})P(z_{i} \mathrm{が最大}|z_{i},\alpha_{1,..,m})dz_{i}$ を計算する．

$\displaystyle \int P(z_i|\alpha_{i})P(z_i \mathrm{が最大}|z_i,\alpha_{1,..,m})dz_i = \int\exp(-(z_i-\log\alpha_i)-\exp(-(z_i-\log\alpha_i)))\prod_{j\neq i}\exp(-\exp(-(z_i-\log\alpha_j)))dz_i$

ここで $\prod_{j\neq i}$ と $P(z_i|\alpha_i)$ の $\exp(-\exp(-(z_i-\log\alpha_i)))$ の項をくくると $\prod_{j}$ でまとめて書ける．

$\displaystyle \int\exp(-(z_i-\log\alpha_i)-\exp(-(z_i-\log\alpha_i)))\prod_{j\neq i}\exp(-\exp(-(z_i-\log\alpha_j)))dz_i \\ \displaystyle= \int\exp(-(z_i-\log\alpha_i))\prod_j\exp(-\exp(-(z_i-\log\alpha_j)))dz_i \\ \displaystyle= \int\exp(-(z_i-\log\alpha_i))\exp(-\sum_j\exp(-(z_i-\log\alpha_j)))dz_i \\ \displaystyle=\int\exp(-(z_i-\log\alpha_i)-\exp(-z_i)\sum_j\exp(\log\alpha_j))dz_i$

4行目は $z_i$ が $\prod_j$ に関係ないことと $\exp$ の掛け算を足し算にして書き直した．後は出てきた積分を計算するだけ．ここはちょっとしたテクニックが必要で $s=\exp(-(z_i+\log\alpha_i))$ という変数変換をするとガンマ分布の確率密度関数の形になるから積分はclosed formに求まって最終的には

$\displaystyle P(z_i \mathrm{が最大} | \alpha_{1,..,m}) = \frac{\exp(\log\alpha_i)}{\sum_j\exp(\log\alpha_j)}=\frac{\alpha_i}{\sum_j\alpha_j}$

となり，元のカテゴリカル分布の値になる．素晴らしい．

Gumbel分布からサンプリング

Gumbel分布を使えばいいのは納得したとして，標準Gumbel分布からサンプリングするのは簡単なのかという疑問が残る．これは逆関数法を使って簡単にできる．分布関数は広義単調増加関数で値が区間(0,1)に一様に分布するため，一般にある確率変数 $X$ が従う分布関数 $F(X)$ は $U=F(X)$ という関係を満たす．ただし， $U$ は $F$ により $X$ から一意にきまり $0\lt U\lt1$ の範囲で値をとる．この時 $F$ に関して $X$ と $U$ は一対一に対応するので分布関数には逆関数が存在する．すると $X=F^{-1}(U)$ から $X$ は $F^{-1}$ により $U$ から一意に決まることがわかる．よって， $U\sim\mathrm{Uniform}(0,1)$ のように一様分布からサンプリングすることで任意の確率変数を一様分布からサンプリングできる．以上が逆関数法．標準Gumbel分布の分布関数の逆関数は $F^{-1}(x)=-\log(-\log(x))$ となるため