はじめに

The Concrete Distribution: A Continuous Relaxation of Discrete Random Variablesを読んだのでメモ． ICLR2017の論文でGumbel Max Trickをベースに離散分布を連続分布に緩和することでVAEなどに応用しようというもの．Gumbel Max Trickについては以前に記事を書いた．

Concrete: CONtinuous relaxation of disCRETE

VAEでは正規分からサンプリングする際，reparameterization trickを使って微分可能な形でサンプリングをすることで正規分布をデータの分布として仮定したautoencoderを学習した．今回読んだ論文では正規分布のような連続分布ではなく離散分布（カテゴリカル分布）をデータの分布として仮定したいというもの．

カテゴリカル分布からのサンプリングにはGumbel Max Trickを使った方法がある．Gumbel Max TrickではGumbel分布からサンプリングされた摂動をカテゴリカル分布に加え，argmaxを取ることでカテゴリカル分布からサンプリングを行う．しかしargmaxの処理が入ってしまうため，backpropで勾配を計算する際にargmaxが取られたインデックスにしか勾配が伝播しないので，分布を正しく学習することができないという問題がある．そこでカテゴリカル分布を連続になるように緩和することで解決しようというのがConcrete: CONtinuous relaxation of disCRETE．別な言い方をすれば，Gumbel Max Trickでサンプリングされた値はone-hotベクトルになってしまう，すなわち単体上の頂点に位置するため，これを単体の内部に行くようにしようと言うのがconcrete．以下が例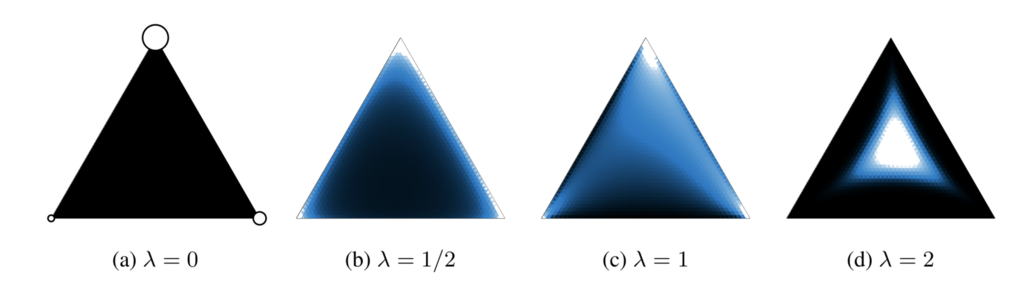． f:id:peluigi:20180623135205p:plain

どのように緩和するかという問題だが，argmaxの代わりにsoftmaxを使うだけ．とても単純．

$\displaystyle X = \mathrm{arg}\max(\alpha_k + G_k) \\ \displaystyle X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$

$\alpha_k$ はカテゴリカル分布のパラメータで $G_k$ は標準Gumbel分布からサンプリングされた値．重要なのが温度パラメータ $\lambda$ でこの値によって緩和の具合が変わる(上の図が $\lambda$ を変化させた時の例．大きくなるほど単体の中心に近付く)．上記緩和を使えばbackpropで勾配が伝播するので（誤解を招く言い方かもしれないが）分布の形状を正しく学習できる．上記の緩和を計算グラフにすると以下． f:id:peluigi:20180623140237p:plain このように確率分布からのサンプリングのノードが入った計算グラフをstochastic computation graphsというらしい．

ここで問題なのはargmaxを勝手にsoftmaxにしてしまったため，もはや確率変数 $X_k$ はカテゴリカル分布に従わない．そこで $X_k$ をconcrete random variableとし，この確率変数が従う分布Concrete Distributionを導入する．Concrete Distributionの密度関数は以下で定義される．

$\displaystyle p_{\alpha,\lambda}(x)=(n-1)!\lambda^{n-1}\prod_{k=1}^n\left(\frac{\alpha_kx_k^{-\lambda-1}}{\sum_{i=1}^n\alpha_ix_i^{-\lambda}}\right)$

この密度分布は以下のpropositionを満たす．

(a) (Reparametarization) $G_k\sim \mathrm{Gumbel}$ が $i.i.d$ なら $X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$

(b) (Rounding) $P(X_k\gt X_i$ $for$ $i\neq k)=\alpha_k/\sum_{I=1}^n\alpha_i$

(d) (Convex eventually) $\lambda\leq (n-1)^{-1}$ なら $p_{\alpha,\lambda}(x)$ はlog-convex

(a)に関してはそもそも $X_k = \frac{\exp( (\log\alpha_k+G_k)/\lambda)}{\sum_i^n\exp( (\log\alpha_i+G_i)/\lambda)}$ から定義されているので成り立つ．(b)と(c)も計算から求まって，元のカテゴリカル分布と一致する．(d)の証明に関してはスペースを使うので論文のAppendix参照．ただし(d)は重要で温度パラメータを決める一つの指標になる．

また，ここでは詳細は省くが，2クラスの場合(binary case)の導出も行なっており，その際には標準Gumbel分布ではなくLogistic分布からのサンプリング結果を摂動として与える(Gumbel分布の差がLogistic分布になるからとのこと)．

VAEへの応用

VAEへの応用を考える．カテゴリカル分布を使った際の損失関数は以下のようになる．

$\displaystyle L_1(\theta,a,\alpha)=\mathbb{E}_{D\sim Q_\alpha(d|x)} \left[\log\frac{p_\theta(x|D)P_a(D)}{Q_\alpha(D|x)}\right]$

$Q_\alpha$ は近似事後分布で $\alpha$ をパラメータとしたカテゴリカル分布．分子はカテゴリ $d$ とデータ $x$ の同時分布 $p_{\theta,\alpha}(x,d)=p_\theta(x|D)P_a(D)$ を表しており， $P_a(D)$ は $a$ をパラメータとするカテゴリカル分布．これをConcrete distributionを使って緩和することを考える．具体的には $D\sim \mathrm{Discrete}(\alpha(x))$ を $Z\sim \mathrm{Concrete}(\alpha(x),\lambda_1)$ とすることを考える．問題は，backpropを行うことができればいいため損失関数の緩和の方法は以下のように複数考えられる．

$\displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \\ \displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) +\sum_{i=1}^nZ_i \log\frac{p_{a}(d^{(i)})}{Q_{\alpha}(d^{(i)}|x)}\right] \\ \displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) \right] +\sum_{i=1}^nQ_\alpha(d^{(i)}|x) \log\frac{p_{a}(d^{(i)})}{Q_{\alpha}(d^{(i)}|x)}$

$d^{(i)}$ は $d_i^{(i)}=1$ を満たすone-hotベクトル．上記において一番上のみが以下のlower boundを保証する．

$\displaystyle \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \leq \log\int p_\theta(x|z)p_{a,\lambda_2}(z)dx$

基本的にはいずれかの緩和された損失を適用すればいいが，愚直に用いるとunderflowを起こしてしまうので実装の際には以下のようにlog-spaceで計算を行う方がいいらしい．

$\displaystyle Y_k=\frac{\log\alpha_k+G_k}{\lambda}-\log\sum_{i=1}^n\exp\left\{\frac{\log\alpha_i+G_i}{\lambda}\right\} \\ \displaystyle \exp(Y)\sim Concrete(\alpha,\lambda) \\ \displaystyle Y\sim \mathrm{ExpConcrete}(\alpha,\lambda)$

またこの確率変数 $Y_k$ の密度関数（log-density）は以下で定義される．

$\displaystyle \log\kappa_{\alpha,\lambda}(y)=\log( (n-1)!)+(n-1)\log\lambda+\left(\sum_{k=1}^n\log\alpha_k-\lambda y_k\right)-n\log\sum_{k=1}^n\exp(\log\alpha_k-\lambda y_k)$

ということで実践的には上記のExpConcreteを使って緩和を行う．すると緩和された損失関数は以下のようになる．

$\displaystyle L_1(\theta,a,\alpha)\overset{\mathrm{relax}}{\leadsto} \\ \displaystyle = \mathbb{E}_{Z\sim q_{\alpha,\lambda_1}(z|x)} \left[\log p_\theta(x|Z) + \log\frac{p_{a,\lambda_2}(Z)}{q_{\alpha,\lambda_1}(Z|x)}\right] \\ \displaystyle = \mathbb{E}_{Y\sim\kappa_{\alpha,\lambda_1}(y|x)}\left[\log p_\theta(x|\exp(Y)) + \log\frac{\rho_{a,\lambda_2}(Y)}{\kappa_{\alpha,\lambda_1}(Y|x)}\right]$

この損失関数を使えばカテゴリカル分布をつかったVAEの学習ができる．論文のAppendixの最後にここで説明したConcreteとExpConcreteのほかに2クラスの場合(Binary case)のBinConcreteや実験で使われた分布がまとまったチートシートが書かれているので便利．またその他Appendixに実装の際や問題に適用する際のTipsが色々書いてあるので参考に．